Fragility, stability and clinical relevance.

Blinders are pieces that are put over the eyes of some draft animals, such as donkeys or horses. Its purpose is none other than to get the animal to focus only on the road ahead, without being distracted by other things that it could see through its peripheral vision, less important for its task.
I always feel a bit sad to see them like that, pulling the chariot with his eyes half covered. But, making an effort, I can understand the usefulness of the device, especially in areas with heavy traffic, where the animal could be frightened if it could see everything it has around it.
And this issue leads me to think of other blinders, a symbolic ones this time, that so-called human beings wear on many occasions, limiting their vision and, on many occasions, without a clear benefit. I’m referring this time to the obsesion for statistical significance, one of those blinders that someone put on us at some time and that we should take off to get a bigger picture.
When we read a clinical trial, it is a very common custom to look for the p-value to see if it is statistically significant, even before looking at the result of the study outcome variable and evaluating the methodological quality of the trial. Leaving aside the clinical relevance of the results (to which we will return shortly), this is not a recommended practice.
First, the significance threshold is totally arbitrary, and moreover, we always have a probability of making an error, whatever we do after knowing the p-value. Furthermore, the value of p depends, among other factors, on the sample size and the number of effects we observe, which can also vary by chance.
Fragility, stability, and relevance
In this sense, we already saw in a previous post how some authors thought of developing a fragility index, which gives an approximation of how the p-value and its statistical significance could be modified, if some of the trial participants had had another outcome.
The fragility index would thus be defined as the minimum number of changes in the participants’ results that would change the statistical significance of the trial (from significant to non-significant, and vice versa). Studies with a lower index values would be considered more fragile, as minor modifications of the results would eliminate their significance.
This new approach has the merit of not basing the assessment of the study solely on the p-value obtained. In general, we will feel more comfortable the higher the fragility index since it would take many more changes for the p to stop being significant. However, we are forgetting two fundamental aspects. First, how likely it is that these changes in the results will occur. Second, the clinical relevance of the effect size observed in the study.
Let’s see an example
Let’s suppose that we do a clinical trial to assess two treatment alternatives for that terrible disease that is fildulastrosis. In order to not to fret over drugs names, we are going to call these two alternatives A and B.
We recruited 295 patients and distributed them randomly between the two arms of the trial, 145 for treatment A and 150 for treatment B.
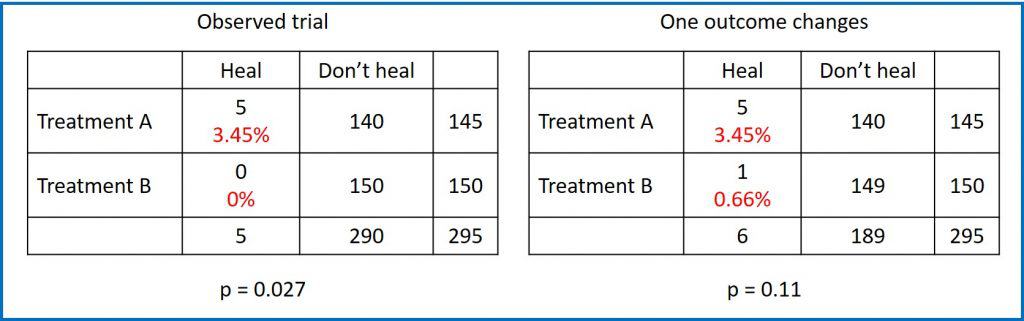
At the end of the study we obtain the results that you can see in the first contingency table. In group A, 5 patients were healed, while in group B none were healed. The probability of being healed in group A was therefore 3.45%, while that of B was 0%. At first glance, it seems that there was a greater probability of being healed in group A and, indeed, if we perform a Fisher’s exact test it gives us a value of p = 0.027 for a bilateral contrast.
As a conclusion, being p <0.05, we reject the null hypothesis which, for Fisher’s test, assumes that the probability of healing is equal in the two groups. In other words, there is a statistically significant difference, so we conclude that treatment A was more effective in healing fildulastrosis.
Fragility
But what if a participant in group B had been healed? You can see it in the second contingency table.
The probability of being healed in group A would continue to be 3.45%, while that of B would be, in this case, 0.66%. It appears that A is still better, but if we do Fisher’s exact test again, the p-value for a two-sided test is now 0.11.
What happened? The difference is no longer statistically significant only with the change in the outcome of one of the 295 participants. The fragility index would be equal to 1, with which we would consider the initial result as fragile.
Now I ask myself: are we considering everything that we should? I would say not. Let’s see.
Stability
Our initial study, if we rely solely on the fragility index, would be considered fragile, which we could express as having an unstable statistical significance.
But this argument is a bit fallacious, since we are not taking into account how likely it is that this change will occur in one of the participants.
Suppose that, from previous studies, we know that the probability of healing the disease without treatment is 0.1%. We can use a binomial probability calculator to make a few numbers. For example, the probability that none of the 150 (the first assumption) will be healed is 86%. Similarly, the probability that exactly 1 is healed is 13%.
And this is where the fallacy lies: we are assessing the fragility of statistical significance by comparing the result that we have observed with another eventual one whose probability of occurrence is much lower. As a conclusion, it does not seem reasonable to define the fragility of the finding without assessing the likelihood of producing this minimal change that modifies the statistical significance.
Now imagine that the probability of being healed without treatment was 1%. The probability of not observing any healing with 150 patients would be 22%, while that of exactly 1 heals rises to 33%. Here we could say that the study provides a fragile significance (that alternative outcome is most likely than the observed one).
Clinical relevance
To finish doing things well and really widen our field of vision, we should not be satisfied only with statistical significance, but we should also assess the clinical relevance of the result.
In this sense, some authors have proposed that, before calculating the statistical significance of the observed effect, the clinically relevance threshold should have been established. Thus, the minimum important difference between the two groups is defined.
If the effect we detect exceeds this minimal difference between the two groups, we can say that the effect is quantitatively significant. This quantitative significance has nothing to do with statistical significance, it only implies that the observed effect is greater than that considered important from a clinical point of view.
In order not to get confused with the two meanings, we are going to call this quantitative significance what its true name: clinical relevance.
Back to the topic: fragility, stability, and importance
We are going to try to put togethe the three aspects that we have dealt with so far.
If the p-value of the observed effect is less than 0.05, we can start by stating that this difference is statistically significant. Next, we will consider the fragility and clinical relevance of the result.
If the effect is not clinically relevant it will not make sense to spend more time on it, even if the p is significant.
But if the effect is clinically relevant, now we will no longer be content with calculating how many changes have to occur to modify statistical significance (and how likely it is that those changes will occur), but we will have to calculate how many changes must occur to lose that minimal clinically relevant difference.
If that number is greater than the fragility index, the result may be statistically unstable, but stable from the point of view of the clinical significance of the result.
On the contrary, a slight change in the outcomes will make the magnitude of the effect considered relevant disappear if the study is quantitatively unstable. If these changes can occur with a reasonably high probability, we will not have much confidence in the results of the study, regardless of their statistical significance.
In summary
To summarize everything we have said, when the time comes to assess the results of a clinical trial, we can follow these four steps:
- Assess statistical significance. Here we must not lose sight of the fact that reaching significance may be a matter of increasing the sample size sufficiently.
- Determine the clinical significance. The reference is the minimum relevant difference that we want to observe between the two groups, taking into account the criteria of clinical relevance of the effect.
- Assess quantitative stability. Determine the number of changes that can modify the clinical significance of the results.
- Determine if the study is fragile or stable. How many changes are needed to reverse statistical significance (the fragility index that we started this whole thing with).
We are leaving…
And here we are going to end this post, long and thick, but one that deals with an important issue that our blinders prevent us from assessing properly.
All of the above refers to clinical trials, although this problem can also be applied to meta-analyzes, where the overall outcome measure can also radically change with changes in the results of some of the primary studies in the review. For this reason, some indices have also been developed, such as Ronsenthal’s safe N or, also considering the clinical relevance, Orwin’s safe N. But that is another story…