Management of non-normal data.

When we are dealing with the management of non-normal data, we must use other strategies to make a hypotheses contrast.
According to the dictionary, one thing is considered normal when it’s in its natural state or conforms to standards set in advance. And this is its normal meaning. But, like many other words, “normal” has many other meanings. In statistics, we talking about normal we refer to a given probability distribution that is called the normal distribution, the famous Gauss’ bell.
This distribution is characterized by its symmetry around its mean that coincides with its median, in addition to other features which we discussed in a previous post. The great advantage of the normal distribution is that it allows us to calculate probabilities of occurrence of data from this distribution, which results in the possibility of inferring population data using a sample obtained from it.
Data do not always follow a normal distribution
Thus, virtually all parametric techniques of hypothesis testing need that data follow a normal distribution. One might think that this is not a big problem. If it’s called normal it’ll be because biological data do usually follow, more or less, this distribution. Big mistake, many data follow a distribution that deviates from normal.
Consider, for example, the consumption of alcohol. The data will not be grouped symmetrically around a mean. In contrast, the distribution will have a positive bias (to the right): there will be a large number around zero (abstainers or very occasional drinkers) and a long right tail formed by people with higher consumption. The tail is long extended to the right with the consumption values of those people who eat breakfast with bourbon.
And how affect our statistical calculations the fact that the variable doesn’t follow a normal?. What should we do if data are not normal?.
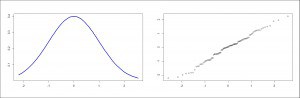
Another possibility is to use numeric contrast tests such as the Shapiro-Wilk’s or the Kolmogorov-Smirnov’s. The problem with these tests is that they are very sensitive to the effect of sample size. If the sample is large they can be affected by minor deviations from normality. Conversely, if the sample is small, they may fail to detect large deviations from normality. But these tests also have another drawback you will understand better after a small clarification.
What to do if non-normal data
We know that in any hypothesis testing we set a null hypothesis that usually says the opposite of what we want to show. Thus, if the value of statistical significance is lower than a set value (usually 0.05), we reject the null hypothesis and stayed with the alternative, that says what we want to prove. The problem is that the null hypothesis is only falsifiable, it can never be said to be true. Simply, if the statistical significance is high, we cannot say it’s untrue, but that does not mean it’s true. It may happen that the study did not have enough power to reject a null hypothesis that is, in fact, false.
Well, it happens that contrasts for normality are set with a null hypothesis that the data follow a normal. Therefore, if the significance is small, we can reject the null and say that the data are not normal. But if the significance is high, we simply cannot reject it and we will say that we have no ability to say that the data are not normal, which is not the same as to say that the fit a normal distribution. For these reasons, it is always advisable to complement numerical contrasts with some graphical method to test the normality of the variable.
Once we know that the data are not normal, we must take this into account when describing them. If the distribution is highly skewed we cannot use the mean as a measure of central tendency and we must resort to other robust estimators such as the median or other parameters available for these situations.
Furthermore, the absence of normality may discourage the use of parametric contrast tests. Student’s t test and the analysis of variance (ANOVA) require that the distribution is normal. Student’s t is quite robust in this regard, so that if the sample is large (n> 80) it can be used with some confidence. But if the sample is small or very different from the normal, we cannot use parametric contrast tests.
One of the possible solutions to this problem would be to attempt a data transformation. The most frequently used in biology is the logarithmic transformation, useful to approximate to a normal distribution when the distribution is right-skewed. We mustn’t forget to undo the transformation once the contrast in question has been made.
Non-parametric tests
he other possibility is to use nonparametric tests, which require no assumption about the distribution of the variable. Thus, to compare two means of unpaired data we will use the Wilcoxon’s rank sum test (also called Mann-Whitney’s U test). If data are paired we will have to use the Wilcoxon’s sign rank test. If we compare more than two means, the Kruskal-Wallis’ test will be the nonparametric equivalent of the ANOVA. Finally, remember that the nonparametric equivalent of the Pearson’s correlation coefficient is the Spearman’s correlation coefficient.
The problem is that nonparametric tests are more demanding than their parametric equivalent to obtain statistical significance, but they must be used as soon as there’s any doubt about the normality of the variable we’re contrasting.
We’re leaving
And here we will stop for today. We could have talked about a third possibility of facing a not-normal variable, much more exotic than those mentioned. It is the use of resampling techniques such as bootstrapping, which consists of building an empirical distribution of the means of many samples drawn from our data to make inferences with the results, thus preserving the original units of the variable and avoiding the swing of data transformation techniques. But that’s another story…
