Randomized clinical trial.

The components of parallel randomized clinical trial are described, as well as the most common design variants (crossover, sequential, community trials).
There is no doubt that when doing a research in biomedicine we can choose from a large number of possible designs, all with their advantages and disadvantages. But in such a diverse and populous court, among jugglers, wise men, gardeners and purple flautists, it reigns over all of them the true Crimson King in epidemiology: the randomized clinical trial.
Definition of randomized clinical trial
The clinical trial is an interventional analytical study, with antegrade direction and concurrent temporality, and with sampling of a closed cohort with control of exposure. In a trial, a sample of a population is selected and divided randomly into two groups. One of the groups (intervention group) undergoes the intervention that we want to study, while the other (control group) serves as a reference to compare the results. After a given follow-up period, the results are analyzed and the differences between the two groups are compared. We can thus evaluate the benefits of treatments or interventions while controlling the biases of other types of studies: randomization favors that possible confounding factors, known or not, are distributed evenly between the two groups, so that if in the end we detect any difference, this has to be due to the intervention under study. This is what allows us to establish a causal relationship between exposure and effect.
From what has been said up to now, it is easy to understand that the randomized clinical trial is the most appropriate design to assess the effectiveness of any intervention in medicine and is the one that provides, as we have already mentioned, a higher quality evidence to demonstrate the causal relationship between the intervention and the observed results.
But to enjoy all these benefits it is necessary to be scrupulous in the approach and methodology of the trials. There are checklists published by experts who understand a lot of these issues, as is the case of the CONSORT list, which can help us assess the quality of the trial’s design. But among all these aspects, let us give some thought to those that are crucial for the validity of the clinical trial.
Components of randomized clinical trials
Everything begins with a knowledge gap that leads us to formulate a structured clinical question. The only objective of the trial should be to answer this question and it is enough to respond appropriately to a single question. Beware of clinical trials that try to answer many questions, since, in many cases, in the end they do not respond well to any. In addition, the approach must be based on what the inventors of methodological jargon call the equipoise principle, which does not mean more than, deep in our hearts, we do not really know which of the two interventions is more beneficial for the patient (from the ethical point of view, it would be necessary to be anathema to make a comparison if we already know with certainty which of the two interventions is better). It is curious in this sense how the trials sponsored by the pharmaceutical industry are more likely to breach the equipoise principle, since they have a preference for comparing with placebo or with “non-intervention” in order to be able to demonstrate more easily the efficacy of their products.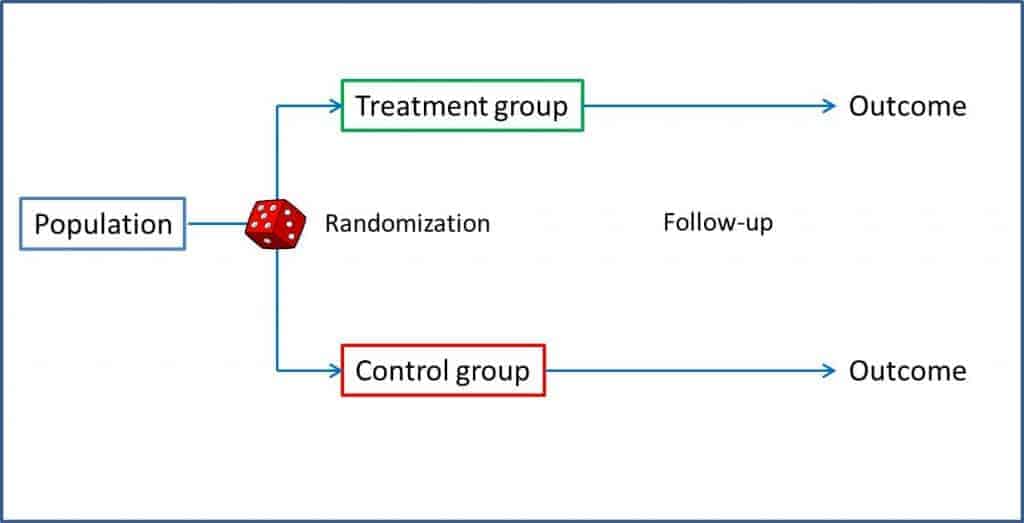
Randomization is one of the key points of the clinical trial. It is the one that assures us that we can compare the two groups, since it tends to distribute the known variables equally and, more importantly, also the unknown variables between the two groups. But do not relax too much: this distribution is not guaranteed at all, it is only more likely to happen if we randomize correctly, so we should always check the homogeneity of the two groups, especially with small samples.
In addition, randomization allows us to perform masking appropriately, with which we perform an unbiased measurement of the response variable, avoiding information biases. These results of the intervention group can be compared with those of the control group in three ways. One of them is to compare with a placebo. The placebo should be a preparation of physical characteristics indistinguishable from the intervention drug but without its pharmacological effects. This serves to control the placebo effect (which depends on the patient’s personality, their feelings towards the intervention, their love for the research team, etc.), but also the side effects that are due to the intervention and not to the pharmacological effect (think, for example, of the percentage of local infections in a trial with medication administered intramuscularly).
The other way is to compare with the accepted as the most effective treatment so far. If there is a treatment that works, the logical (and more ethical) is that we use it to investigate whether the new one brings benefits. It is also usually the usual comparison method in equivalence or non-inferiority studies. Finally, the third possibility is to compare with non-intervention, although in reality this is a far-fetched way of saying that only the usual care that any patient would receive in their clinical situation is applied.
It is essential that all participants in the trial are submitted to the same follow-up guideline, which must be long enough to allow the expected response to occur. All losses that occur during follow-up should be detailed and analyzed, since they can compromise the validity and power of the study to detect significant differences. And what do we do with those that get lost or end up in a different branch to the one assigned? If there are many, it may be more reasonable to reject the study. Another possibility is to exclude them and act as if they had never existed, but we can bias the results of the trial. A third possibility is to include them in the analysis in the branch of the trial in which they have participated (there is always one that gets confused and takes what he should not), which is known as analysis by treatment or analysis by protocol. And the fourth and last option we have is to analyze them in the branch that was initially assigned to them, regardless of what they did during the study. This is called the intention-to-treat analysis, and it is the only one of the four possibilities that allows us to retain all the benefits that randomization had previously provided.
Data analysis
As a final phase, we would have the analyze and compare the data to draw the conclusions of the trial, using for this the association and impact measures of effect that, in the case of the clinical trial, are usually the response rate, the risk ratio (RR), the relative risk reduction (RRR), the absolute risk reduction (ARR) and the number needed to treat (NNT). Let’s see them with an example.
Let’s imagine that we carried out a clinical trial in which we tried a new antibiotic (let’s call it A not to get warm from head to feet) for the treatment of a serious infection of the location that we are interested in studying. We randomize the selected patients and give them the new drug or the usual treatment (our control group), according to what corresponds to them by chance. In the end, we measure how many of our patients fail treatment (present the event we want to avoid).
Thirty six out of the 100 patients receiving drug A present the event to be avoided. Therefore, we can conclude that the risk or incidence of the event in those exposed (Ie) is 0.36. On the other hand, 60 of the 100 controls (we call them the group of not exposed) have presented the event, so we quickly calculate that the risk or incidence in those not exposed (Io) is 0.6.
At first glance we already see that the risk is different in each group, but as in science we have to measure everything, we can divide the risks between exposed and not exposed, thus obtaining the so-called risk ratio (RR = Ie / Io). An RR = 1 means that the risk is equal in the two groups. If the RR> 1 the event will be more likely in the group of exposed (the exposure we are studying will be a risk factor for the production of the event) and if RR is between 0 and 1, the risk will be lower in those exposed. In our case, RR = 0.36 / 0.6 = 0.6. It is easier to interpret RR> 1. For example, a RR of 2 means that the probability of the event is twice as high in the exposed group. Following the same reasoning, a RR of 0.3 would tell us that the event is a third less frequent in the exposed than in the controls. You can see in the attached table how these measures are calculated.
But what we are interested in is to know how much the risk of the event decreases with our intervention to estimate how much effort is needed to prevent each one. For this we can calculate the RRR and the ARR. The RRR is the risk difference between the two groups with respect to the control (RRR = [Ie-Io] / Io). In our case it is 0.4, which means that the intervention tested reduces the risk by 60% compared to the usual treatment.
The ARR is simpler: it is the difference between the risks of exposed and controls (ARR = Ie – Io). In our case it is 0.24 (we ignore the negative sign), which means that out of every 100 patients treated with the new drug there will be 24 fewer events than if we had used the control treatment. But there is still more: we can know how many we have to treat with the new drug to avoid an event by just doing the rule of three (24 is to 100 as 1 is to x) or, easier to remember, calculating the inverse of the ARR. Thus, the NNT = 1 / ARR = 4.1. In our case we would have to treat four patients to avoid an adverse event. The context will always tell us the clinical importance of this figure.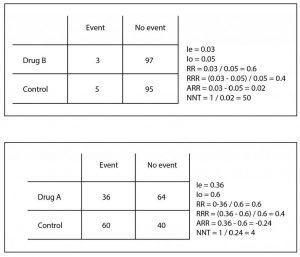
As you can see, the RRR, although it is technically correct, tends to magnify the effect and does not clearly quantify the effort required to obtain the results. In addition, it may be similar in different situations with totally different clinical implications. Let’s see it with another example that I also show you in the table. Suppose another trial with a drug B in which we obtain three events in the 100 treated and five in the 100 controls. If you do the calculations, the RR is 0.6 and the RRR is 0.4, as in the previous example, but if you calculate the ARR you will see that it is very different (ARR = 0.02), with an NNT of 50 It is clear that the effort to avoid an event is much greater (4 versus 50) despite the same RR and RRR.
So, at this point, let me advice you. As the data needed to calculate RRR are the same than to calculate the easier ARR (and NNT), if a scientific paper offers you only the RRR and hide the ARR, distrust it and do as with the brother-in-law who offers you wine and cured cheese, asking him why he does not better put a skewer of Iberian ham. Well, I really wanted to say that you’d better ask yourselves why they don’t give you the ARR and compute it using the information from the article.
Basic design modifications
So far all that we have said refers to the classical design of parallel clinical trials, but the king of designs has many faces and, very often, we can find papers in which it is shown a little differently, which may imply that the analysis of the results has special peculiarities.
Let’s start with one of the most frequent variations. If we think about it for a moment, the ideal design would be that which would allow us to experience in the same individual the effect of the study intervention and the control intervention (the placebo or the standard treatment), since the parallel trial is an approximation that it assumes that the two groups respond equally to the two interventions, which always implies a risk of bias that we try to minimize with randomization. If we had a time machine we could try the intervention in all of them, write down what happens, turn back the clock and repeat the experiment with the control intervention so we could compare the two effects. The problem, the more alert of you have already imagined, is that the time machine has not been invented yet.
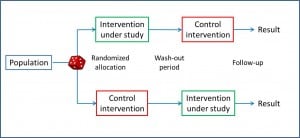
It is also necessary to consider whether the order of the interventions can affect the final result (sequence effect), with which only the results of the first intervention would be valid. Another problem is that, having a longer duration, the characteristics of the patient can change throughout the study and be different in the two periods (period effect). And finally, beware of the losses during the study, which are more frequent in longer studies and have a greater impact on the final results than in parallel trials.
Imagine now that we want to test two interventions (A and B) in the same population. Can we do it with the same trial and save costs of all kinds? Yes, we can, we just have to design a factorial clinical trial. In this type of trial, each participant undergoes two consecutive randomizations: first it is assigned to intervention A or to placebo (P) and, second, to intervention B or placebo, with which we will have four study groups: AB, AP, BP and PP. As is logical, the two interventions must act by independent mechanisms to be able to assess the results of the two effects independently.
Usually, an intervention related to a more plausible and mature hypothesis and another one with a less contrasted hypothesis are studied, assuring that the evaluation of the second does not influence the inclusion and exclusion criteria of the first one. In addition, it is not convenient that neither of the two options has many annoying effects or is badly tolerated, because the lack of compliance with one treatment usually determines the poor compliance of the other. In cases where the two interventions are not independent, the effects could be studied separately (AP versus PP and BP versus PP), but the design advantages are lost and the necessary sample size increases.
At other times it may happen that we are in a hurry to finish the study as soon as possible. Imagine a very bad disease that kills lots of people and we are trying a new treatment. We want to have it available as soon as possible (if it works, of course), so after every certain number of participants we will stop and analyze the results and, in the case that we can already demonstrate the usefulness of the treatment, we will consider the study finished. This is the design that characterizes the sequential clinical trial. Remember that in the parallel trial the correct thing is to calculate previously the sample size. In this design, with a more Bayesian mentality, a statistic is established whose value determines an explicit termination rule, so that the size of the sample depends on the previous observations. When the statistic reaches the predetermined value we see ourselves with enough confidence to reject the null hypothesis and we finish the study. The problem is that each stop and analysis increases the error of rejecting it being true (type I error), so it is not recommended to do many intermediate analysis. In addition, the final analysis of the results is complex because the usual methods do not work, but there are others that take into account the intermediate analysis. This type of trial is very useful with very fast-acting interventions, so it is common to see them in titration studies of opioid doses, hypnotics and similar poisons.
Clustered trials
There are other occasions when individual randomization does not make sense. Imagine we have taught the doctors of a center a new technique to better inform their patients and we want to compare it with the old one. We cannot tell the same doctor to inform some patients in one way and others in another, since there would be many possibilities for the two interventions to contaminate each other. It would be more logical to teach the doctors in a group of centers and not to teach those in another group and compare the results. Here what we would randomize is the centers to train their doctors or not. This is the trial with group assignment design. The problem with this design is that we do not have many guarantees that the participants of the different groups behave independently, so the size of the sample needed can increase a lot if there is great variability between the groups and little within each group. In addition, an aggregate analysis of the results has to be done, because if it is done individually, the confidence intervals are falsely narrowed and we can find false statistical meanings. The usual thing is to calculate a weighted synthetic statistic for each group and make the final comparisons with it.
The last of the series that we are going to discuss is the community essay, in which the intervention is applied to population groups. When carried out in real conditions on populations, they have great external validity and often allow for cost-efficient measures based on their results. The problem is that it is often difficult to establish control groups, it can be more difficult to determine the necessary sample size and it is more complex to make causal inference from their results. It is the typical design for evaluating public health measures such as water fluoridation, vaccinations, etc.
We’re leaving…
I’m done now. The truth is that this post has been a bit long (and I hope not too hard), but the King deserves it. In any case, if you think that everything is said about clinical trials, you have no idea of all that remains to be said about types of sampling, randomization, etc., etc., etc. But that is another story…
