Fragilidad, estabilidad e importancia clínica.

Las anteojeras son unas piezas que se le ponen sobre los ojos a algunos animales de tiro, como los burros o los caballos. Su finalidad no es otra que conseguir que el animal se centre solo en el camino que tiene delante, sin distraerse con otras cosas que podría ver por su visión periférica, menos importantes para su tarea.
A mí siempre me da un poco de pena verlos, tirando del carro y con los ojos medio tapados, pero, haciendo un esfuerzo, puedo comprender la utilidad del artilugio, sobre todo en zonas con mucho tránsito, donde el animal podría asustarse si pudiese ver todo lo que tiene a su alrededor.
Y este asunto me lleva a pensar en otras anteojeras, simbólicas esta vez, que los llamados seres humanos nos calzamos en muchas ocasiones, limitando nuestra visión y, en muchas ocasiones, sin un beneficio claro. Me estoy refiriendo esta vez a la fijación por la significación estadística, una de esas anteojeras que alguien nos puso en algún momento y que deberíamos quitarnos para tener una visión más amplia.
Cuando leemos un ensayo clínico, es una costumbre muy habitual buscar el valor de la p para ver si es estadísticamente significativa, incluso antes de mirar cuál es el resultado de la variable de estudio y de evaluar la calidad metodológica del trabajo. Dejando a un lado la importancia clínica de los resultados (a la que volveremos en seguida), esta es una práctica nada recomendable.
En primer lugar, el umbral de significación es totalmente arbitrario y, además, siempre tenemos una probabilidad de cometer un error, hagamos lo que hagamos después de conocer el valor de p. Además, el valor de p depende, entre otros factores, del tamaño muestral y del número de efectos que observemos, que también pueden variar por cuestión de azar.
Fragilidad, estabilidad e importancia
En este sentido, ya vimos en una entrada previa como algunos autores pensaron en elaborar un índice de fragilidad, que nos da idea de cómo se podría modificar el valor de p, y su significación estadística, si algunos de los participantes del ensayo hubiesen tenido otro resultado.
Se definiría así el índice de fragilidad como el número mínimo de cambios en los resultados de los participantes que harían cambiar la significación estadística del ensayo (de significativa a no significativa, y viceversa). Los estudios con un índice más bajo se considerarían más frágiles, ya que mínimas modificaciones de los resultados acabarían con su significación.
Este nuevo enfoque tiene el mérito de no basar la valoración del estudio únicamente en el valor de p obtenido. En general, nos sentiremos más cómodos cuanto mayor sea el índice de fragilidad, ya que harían falta muchos más cambios para que la p dejase de ser significativa. Sin embargo, estamos olvidando dos aspectos fundamentales. El primero, cuanto de probable es que se produzcan esos cambios en los resultados. El segundo, la importancia clínica del tamaño de efecto medido en el estudio.
Veamos un ejemplo
Vamos a suponer que hacemos un ensayo clínico para valorar dos alternativas de tratamiento para esa terrible enfermedad que es la fildulastrosis. Para no calentarnos mucho la cabeza, vamos a llamar A y B a estas dos alternativas.
Reclutamos 295 pacientes y los repartimos al azar entre las dos ramas del ensayo, 145 al tratamiento A y 150 al B.
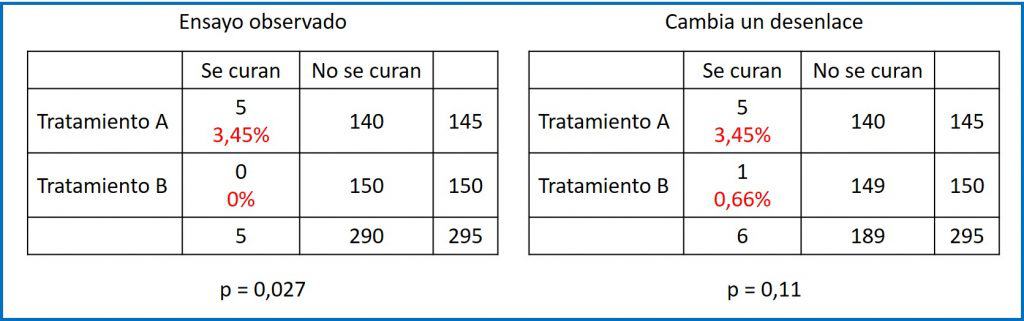
Al finalizar el estudio obtenemos los resultados que podéis ver en la primera tabla de contingencia. En el grupo A se han curado 5 pacientes, mientras que en el grupo B no se ha curado ninguno. La probabilidad de curarse en el grupo A fue, por tanto, del 3,45%, mientras que la del B fue de 0%. A simple vista, parece que hubo mayor probabilidad de curarse en el grupo A y, efectivamente, si realizamos una prueba exacta de Fisher nos da un valor de p=0,027 para un contraste bilateral.
Como conclusión, al ser p < 0,05, rechazamos la hipótesis nula que, para la prueba de Fisher, asume que la probabilidad de curación es igual en los dos grupos. Dicho de otra forma: existe una diferencia estadísticamente significativa, por lo que asumimos que el tratamiento A fue más eficaz para curar la fildulastrosis.
Fragilidad
Pero ¿qué pasaría si en el grupo B se hubiese curado un participante? Podéis verlo en la segunda tabla de contingencia.
La probabilidad de curarse en el grupo A seguiría siendo del 3,45%, mientras que la del B sería, en este caso, de 0,66%. Parece que A sigue siendo mejor, pero si hacemos otra vez la prueba exacta de Fisher, el valor de p para un contraste bilateral ahora es de 0,11.
¿Qué ha pasado? La diferencia ha dejado de ser estadísticamente significativa solo con haber cambiado el resultado de uno de los 295 participantes. El índice de fragilidad sería igual a 1, con lo que consideraríamos el resultado inicial como frágil.
Ahora yo me pregunto: ¿estamos teniendo en cuenta todo lo que deberíamos? Yo diría que no. Veámoslo.
Estabilidad
Nuestro estudio inicial, si nos basamos únicamente en el índice de fragilidad, sería considerado frágil, lo que podríamos expresar como que tiene una significación estadística inestable.
Pero este argumento puede ser un poco falaz, ya que no estamos teniendo en cuenta cómo de probable es que se produzca este cambio en uno de los participantes.
Supongamos que, por estudios previos, sabemos que la probabilidad de curar la enfermedad sin tratamiento es del 0,1%. Podemos utilizar una calculadora de probabilidad binomial para hacer unos pocos números. Por ejemplo, la probabilidad de que no se cure ninguno de los 150 (el primer supuesto) es del 86%. De igual manera, la probabilidad de que se cure exactamente 1 es del 13%.
Y aquí es donde está la falacia: estamos valorando la fragilidad de la significación estadística comparando el supuesto que hemos observado con otro eventual cuya probabilidad de ocurrencia es mucho menor. Como conclusión, no parece razonable definir la fragilidad del hallazgo sin valorar la verosimilitud de que se produzca ese mínimo cambio que nos modifique la significación estadística.
Imaginad ahora que la probabilidad de curarse sin tratamiento fuese del 1%. La probabilidad de no observar ninguna curación con 150 pacientes sería del 22%, mientras que la de que se cure exactamente 1 sube hasta 33%. Aquí si podremos decir que el estudio nos proporciona una significación frágil (es más probable el supuesto imaginado que el resultado observado).
Importancia clínica
Para acabar de hacer las cosas bien y ampliar de verdad nuestro campo de visión, no deberíamos quedarnos solo con la significación estadística, sino que tendríamos que valorar también la importancia clínica del resultado.
En este sentido, algunos autores han propuesto que, antes de calcular la significación estadística del efecto observado, debe haberse establecido cuál es el efecto clínicamente importante. Así, se define la mínima diferencia importante entre los dos grupos.
Si el efecto que detectamos supera esta mínima diferencia entre los dos grupos, podremos decir que el efecto es cuantitativamente significativo. Esta significación cuantitativa no tiene nada que ver con la estadística, solo implica que el efecto observado es superior al considerado como importante desde el punto de vista clínico.
Para no hacernos un lío con las dos significaciones, a esta significación cuantitativa le vamos a llamar como lo que realmente es: importancia clínica.
Volvemos: fragilidad, estabilidad e importancia
Vamos a tratar de poner en funcionamiento, de manera conjunta, los tres aspectos que hemos tratado hasta ahora.
Si el valor de p del efecto observado es menor de 0,05, podremos comenzar por afirmar que esta diferencia es estadísticamente significativa. A continuación, tendremos en cuenta la fragilidad y la importancia clínica del resultado.
Si el efecto no es clínicamente importante no tendrá sentido dedicarle más tiempo, aunque la p sea significativa.
Pero si el efecto es clínicamente importante, ahora ya no nos contentaremos con calcular cuántos cambios tienen que producirse para modificar la significación estadística (y cuánto de probable es que esos cambios se produzcan), sino que deberemos calcular cuántos cambios deben producirse para perder esa diferencia mínima clínicamente importante.
Si ese número es mayor que el índice de fragilidad, el resultado podrá ser inestable desde el punto de vista estadístico, pero estable desde el punto de vista de la importancia clínica del resultado.
Por el contrario, un mínimo cambio en los resultados hará desaparecer la magnitud del efecto considerada importante si el estudio es cuantitativamente inestable. Si esos cambios pueden ocurrir con una probabilidad razonablemente alta, no tendremos mucha confianza en los resultados del estudio, con independencia de su significación estadística.
En resumen
Para resumir todo lo que hemos dicho, llegado el momento de valorar los resultados de un estudio, podemos seguir estos cuatro pasos:
- Valorar la significación estadística. Aquí no debemos perder de vista que alcanzar la significación puede ser cuestión de aumentar el tamaño muestral lo suficiente.
- Determinar la importancia clínica. La referencia es la mínima diferencia importante que queremos observar entre los dos grupos, teniendo en cuenta los criterios de importancia clínica del efecto.
- Evaluar la estabilidad cuantitativa. Determinar el número de cambios que puede modificar la importancia clínica de los resultados.
- Determinar si el estudio es frágil o estable. Cuántos cambios son necesarios para revertir la significación estadística (el índice de fragilidad con el que comenzamos todo este rollo).
Nos vamos…
Y aquí vamos a finalizar esta entrada larga y espesa, pero que trata un tema importante que nuestras anteojeras nos impiden valorar de la forma adecuada.
Todo lo expuesto se refiere a los ensayos clínicos, aunque este problema puede aplicarse también a los metanálisis, en los que también puede cambiar de forma radical la medida global de resultado con cambios en los resultados de algunos de los estudios primarios de la revisión. Por eso se han desarrollado también algunos índices, como el de la N segura de Ronsenthal o, considerando también la importancia clínica, el de la N segura de Orwin. Pero esa es otra historia…